课程内容

《直线的倾斜角与斜率》
在直角坐标系中，过点P的一条直线绕P点旋转，不管旋转多少周，它对x轴的相对位置有几种情形？画图表示。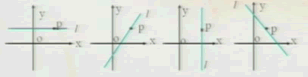

总结：有四种情况，如图。
容易看出，它们的倾斜程度不同，怎样描述直线的倾斜程度呢？
可用直线与x轴所成的角来描述。
直线的倾斜角的定义：
    当直线l与x轴相交时，我们取x轴作为基准，x轴正向与直线l向上方向之间所成的角α叫做直线l的倾斜角。
指出上图中直线的倾斜角是怎样的角：0度角、锐角、直角、钝角
结论：直线的倾斜角α的取值范围为：
      0≤α＜180°
平面直角坐标系内每一条直线都有一个确定的倾斜角，且倾斜程度相同的直线，其倾斜角相等；倾斜程度不同的直线，其倾斜角不相等。因此我们可用倾斜角表示平面直角坐标系内一条直线的倾斜程度。
在平面直角坐标系中，已知直线上的一个点不能确定一条直线的位置。同样，已知直线的倾斜角，也不能确定一条直线的位置，但是，直线上的一点和这条直线的倾斜角可以唯一确定一条直线。
因此，确定平面直角坐标系中一条直线位置的几何要素是：直线上的一个定点以及它的的倾斜角，二者缺一不可。
日常生活中，我们经常用“升高量与前进量的比”表示倾斜面的“坡度”（倾斜程度），即
    坡度（比）=升高量/前进量
思考：倾斜角与坡度比有什么关系？
我们把一条直线的倾斜角α的正切值叫做这条直线的斜率。斜率通常用小写字母k表示，即：
    k=tanα
想一想：
当α=0°时，k值如何？  k=0
当0°＜α＜90°时，k值如何？  k＞0
当α=90°时，k值如何？  k不存在
当90°＜α＜180°时，k值如何？  k＜0
倾斜角α不是90°的直线都有斜率，而且倾斜角不同，直线的斜率也不同。因此，我们可以用斜率表示直线的倾斜程度。
选一选
下列关于直线的倾斜角和斜率的说法，其中______是正确。
A、任一条直线都有倾斜角，也都有斜率    B、直线的倾斜角越大，它的斜率就越大
C、平行于x轴的直线的倾斜角是0或π      D、两直线的斜率相等，它们的倾斜角相等
E、两直线的倾斜角相等，它们的斜率相等  F、直线斜率的范围是（-∞，+∞）
给定两点P₁（x₁，y₁），P₂（x₂，y₂），x₁≠x₂，求直线P₁P₂的斜率k。
学生活动：四组分别计算直线的斜率（用x₁，y₁，x₂，y₂表示）。
思考：当直线P₁P₂与x轴平行或重合时，上述式子还成立吗？为什么？
综上所述，我们得到经过两点P₁（x₁，y₁），P₂（x₂，y₂）（x₁≠x₂）的直线的斜率公式k=（y₁-y₂）/（x₁-x₂）
思考：
1、已知直线上两点A（a₁，a₂），B（b₁，b₂），运用上述公式计算直线AB斜率时，与A、B两点坐标的顺序有关吗？
2、当直线平行于y轴，或与y轴重合时，上述公式还适用吗？为什么？
例1：直线l₁的倾斜角α₁=30°，直线l₂⊥l₁，求l₁、l₂的斜率。
例2：已知A（3,2），B（-4,1），C（0,-1），求直线AB、BC、CA的斜率，并判断这些直线的倾斜角是锐角还是钝角。
例3：在平面直角坐标系中，画出经过原点且斜率分别为1，-1，2及-3的直线l₁，l₂，l₃及l₄。