课程内容:
《指数函数的图象与性质》
一、问题1:有一种细胞分裂时,由1个分裂成2个,2个分裂成4个,4个分裂成8个,……
问题2:《庄子·天下篇》中有一个命题:一尺之棰,日取其半,万世不竭。木棍长度y与经历天数x的关系式是什么?
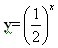
探究:上述问题中的函数解析式有什么共同特征?
·自变量在指数位置
·底数是常量
思考:你能从以上两个解析式中抽象出一个更具有一般性的函数模型吗?
定义:函数y=ax(a>0,且a≠1)叫做指数函数。其中自变量是x,函数的定义域是R。
思考:为什么要规定“a>0,且a≠1”呢?
练习1:判断下列函数中哪些是指数函数?
(1)y=(-2)x______(2)y=2x+1______(3)y=3·4x______
(4)y=10-x______(5)y=2x+1______(6)y=π2x______
例1.已知指数函数f(x)=ax(a>0,且a≠1)的图象经过点(3,π),求f(0)、f(1)、f(-3)的值。
练一练:求下列函数的定义域:
(1)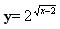 ;(2)
;(2)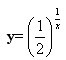
问题3:得到函数的图象一般用什么方法?
列表、描点、连线
探究:用描点法绘制y=2x的草图以及用描点法绘制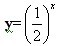 的图象。
的图象。
例2.判断下列函数在(-∞,+∞)内是增函数还是减函数?
(1)y=4x;(2)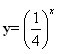 ;(3)
;(3)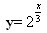 。
。
例3.比较下列各题中两个值的大小:
(1)1.72.5,1.73
(2)0.8-0.1,0.8-0.2
(3)1.70.3,0.93.1
例4.已知下列不等式,比较m,n的大小。
(1)am<an(0<a<1)
(2)am<an(a>1)
例5.设y1=a3x+1,y2=a-2x,其中a>0,a≠1,确定x为何值时,有:
(1)y1=y2;(2)y1>y2;(3)y1<y2。




























