课程内容:
《指数与指数幂的运算》
一、知识回顾
在初中,我们研究了正整数指数幂:一个数a的n次幂等于n个a的连乘积,即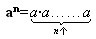
正整数指数幂的运算法则有五条:
1.am·an=am+n;
2.am÷an=am-n;
3.(am)n=amn;
4.(ab)n=an·bn;
5.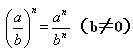
另外,我们规定 a0=1(a≠0);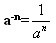
二、根式
一般地,如果xn=a,那么x叫做a的n次方根,其中n>1,且n∈N。
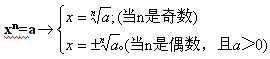
让我们认识一下这个式子: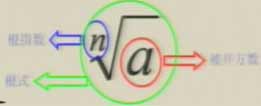
探究: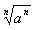 表示an的n次方根,等式
表示an的n次方根,等式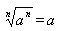 一定成立吗?如果不一定成立,那么
一定成立吗?如果不一定成立,那么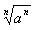 等于什么?
等于什么?
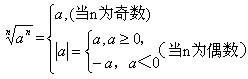
例1.求下列各式的值。
1.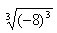 ;2.
;2.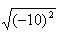 ;3.
;3.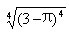 ;4.
;4.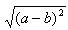 (a>b)。
(a>b)。
三、分数指数幂
探究: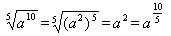 (a>0)
(a>0)
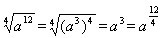 (a>0)
(a>0)
正数的正分数指数幂的意义是,我们规定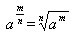 (a>0,m,n∈N,且n>1)
(a>0,m,n∈N,且n>1)
正数的负分数指数幂的意义与负整数指数幂的意义相仿,我们规定: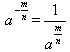 (a>0,m,n∈N,且n>1)
(a>0,m,n∈N,且n>1)
整数指数幂的运算性质对于有理指数幂也同样适用,即对于任意有理数r,s,均有下面的运算性质:
(1)aras=ar+s(a>0,r,s∈Q)
(2)(ar)s=ars(a>0,r,s∈Q)
(3)(ab)r=arbr(a>0,b>0,r∈Q)
例3.计算下列各式。
1.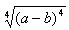 (a<b);2.
(a<b);2.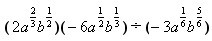 ;3.
;3.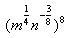 ;4.
;4.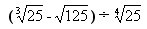 ;5.
;5.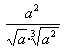 。
。
例4.已知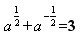 ,求下列各式的值。
,求下列各式的值。
(1)a+a-1;(2)a2+a-2。
练一练:
已知x+x-1=3,求下列各式的值。
(1)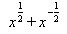 ;(2)
;(2)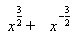 。
。
四、无理指数幂
探究:在前面的学习中,我们已经把指数由正整数推广到了有理数,那么,能不能继续推广到实数范围呢?
一般地,无理数指数幂aα(a>0,α是无理数)是一个确定的实数,有理数指数幂的运算性质同样适用于无理数指数幂。



























