课程内容：
《函数的单调性与最大（小）值（2）》
复习：画出下列函数的草图，并根据图象解答下列问题。
（1）f（x）=-2x+3；（2）f（x）=-x2-2x+1
1.说出y=f（x）的单调区间，以及在各单调区间上的单调性；
2.指出图象的最高点或最低点，并说明它能体现函数的什么特征？
定义：1.最大值
一般地，设函数y=f（x）的定义域为I，如果存在实数M满足：
（1）对于任意的x∈I，都有f（x）≤M；
（2）存在x0∈I，使得f（x0）=M。
那么，称M是函数y=f（x）的最大值。
2.最小值
一般地，设函数y=f（x）的定义域为I，如果存在实数M满足：
（1）对于任意的x∈I，都有f（x）≥M；
（2）存在x0∈I，使得f（x0）=M。
那么，称M是函数y=f（x）的最小值。
注意：1.函数最大（小）值首先应该是某一个函数值，即存在x0∈I，使得f（x0）=M；
2.函数最大（小）值应该是所有函数值中最大（小）的，即对于任意的x∈I，都有f（x）≤M（f（x）≥M）。
例1.“菊花”烟花是最壮观的烟花之一，制造时一般是期望在它达到最高点时爆裂，如果在距离地面高度hm与时间ts之间的关系为：h（t）=-4.9t2+14.7t+18，那么烟花冲出后什么时候是它的爆裂的最佳时刻？这时距地面的高度是多少（精确到1m）？
例2.求函数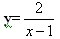
在区间[2,6]上的最大值和最小值。
例3.已知函数f（x）=x2-2x，g（x）=x2-2x（x∈[2,4]）
（1）求f（x）、g（x）的单调区间；
（2）求f（x）、g（x）的最小值。
例4.若函数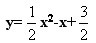
的定义域和值域都是[1，b]（b＞1），求b的值。
