课程内容：
《函数的单调性与最大（小）值（1）》
一、引入新课
观察图像，指出两组函数在性质上的主要区别：
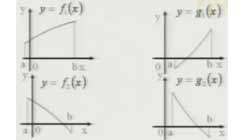
二、分析概念
定义：一般地，设函数f（x）的定义域为I：
1.如果对于定义域I内某个区间D上的任意两个自变量的值x1、x2，当x1＜x2时都有f（x1）＜f（x2），就说函数f（x）在区间D上是增函数；
2.如果对于定义域I内某个区间D上的任意两个自变量的值x1、x2，当x1＜x2时都有f（x1）＞f（x2），就说函数f（x）在区间D上是减函数。
如果函数f（x）在区间D上是增函数或减函数，那么就说函数f（x）在这一区间具有严格的单调性，区间D叫做f（x）的单调区间。
因此，增函数就其本身而言是在相应区间上较大的自变量对应较大的函数值的函数。减函数就其本身而言是在相应区间上较大的自变量对应较小的函数值的函数。
定义中的关键语句有哪些？
1.定义域I内某个区间D取值
增、减函数都是对相应的区间而言的，离开了相应的区间就根本谈不上函数的增减性。
思考：①我们能否说一个函数在x=3时是递增的或是递减的？
②能否脱离区间泛泛而谈某个函数是增函数或是减函数？
所以，在谈论函数增减性时必须指明相应的区间。
2.任意
“任意”就是指不能取特定的值来判断函数的增减性。
3.都有
“都有”是指只要x1＜x2，f（x1）就必须都小于f（x2），或f（x1）都大于f（x2）。
二、概念的应用
例1.根据图像说出函数的单调区间，并回答，在每一个单调区间上，函数是增函数还是减函数？
注意：在函数的几个单调区间之间不能用并集符号连接。
思考：[-5，-2]是函数的单调递减区间，是否（-5，-2）也是函数的单调递减区间？
结论：一般地，若f（x）在[a，b]单调（增或减），且[a1，b1]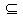
[a，b]，则f（x）在[a1，b1]上单调递（增或减），反之不然。
例2.证明函数f（x）=3x+2在R上是增函数。
总结：判定函数在某区间上的单调性的步骤。
1.设x1，x2是该区间上的任意两个值，且x1＜x2
2.作差f（x1）-f（x2），并变形
3.判定f（x1）-f（x2）的符号
4.根据定义作结论
练习：证明函数图3在（-∞，0）上是减函数。
例3.已知函数f（x）=4x2-ax+5在x∈（-∞，-2）上是减函数，在x∈（-2，+∞）时是增函数，求a。
