课程内容：
《函数的概念（2）》
复习：1.什么叫函数？用什么符号表示函数？
2.什么是函数的定义域？值域？
3.函数f（x）=√1-│x│ 的定义域、值域如何？分别怎样表示？
区间定义：
设a、b是两个实数，而且a＜b，我们规定：
（1）满足不等式a≤x≤b的实数x的集合叫做闭区间，表示[a，b]；
（2）满足不等式a＜x＜b的实数x的集合叫做开区间，表示为（a，b）；
（3）满足不等式a≤x＜b或a＜x≤b的实数x的集合叫做半开半闭区间，分别表示为[a，b），（a，b]。
注意：这里的实数a与b都叫做相应区间的端点。
定义：实数集R可以用区间表示为（-∞，+∞）。“∞”读作“无穷大”，“-∞”读作“负无穷大”，“+∞”读作“正无穷大”。
思考：x≥a，x＞a，x≤b，x＜b的实数x的集合用区间怎么表示？
例题1：将下列集合用区间表示出来。
（1）{x│2x-1≥0}；
（2）{x│x＜-4，或-1＜x≤2}
1.求函数的定义域方法：
（1）f（x）是整式时，则函数的定义域为R。
（2）f（x）是分式时，则函数定义域为使分母不等于0的实数的集合。
（3）二次根式时，则函数定义域是使根号内的式子大于0的实数的集合。
（4）如果f（x）是由几个数学式子构成时，那么函数的定义域是使各部分式子都有意义的实数集合。
例题2：1.求函数f（x）=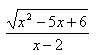
的定义域。
练习1：1.求函数f（x）=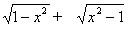
的定义域（ ）。
A.[-1,1] B.(-∞,-1]∪[1,+∞) C.[0,1] D.{-1,+1}
2.复合函数求定义域的几种题型。
题型一：已知f（x）的定义域，求f[g（x）]的定义域。
例题：若f（x）的定义域是[0,2]，求f（2x-1）的定义域。
练习2：若f（x）的定义域是[0,2]，求f（x2）的定义域。
练习3：已知函数f（x）的定义域为（a，b），且b-a＞2，则g（x）=f（3x-1）-f（3x+1）的定义域为___________________。
题型二：已知f[g（x）]的定义域，求f（x）的定义域。
例题3：已知f（2x-1）的定义域(-1,5]，求f（x）的定义域。
练习4：已知f（2x-1）的定义域(-1,5]，求f（2-5x）的定义域。
题型三：已知函数的定义域，求含参数的取值范围。
例题4：当k为何值时，函数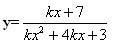
的定义域是一切实数？
