高中数学第一章1.1《集合间的基本关系》（必修1）

课程内容

《集合间的基本关系》
问题提出
1、集合有哪些表示方法？
2、元素与集合有哪几种关系？
3、集合与集合之间又存在哪些关系？
知识探究（一）
考察下列各组集合：
（1）A={1,2,3}与B={1,2,3,4,5}；
（2）A={x|0＜x＜1}与B={x||x|≤1}；
（3）A={x|x是正三角形}与B={x|x是等腰三角形}。
思考1：上述各组集合中，集合A中的元素与集合B有什么关系？
子集的概念：
对于两个集合A，B，如果集合A中任意一个元素都是集合B中的元素，则称集合A为集合B的子集。
我们把不含任何元素的集合叫做空集，记为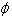，并规定：空集是任何集合的子集。
子集的符号表示：
A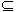B（或B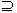A），读作：“A含于B”（或“B包含A”）。
表示示数取值范围的集合，往往用数轴直观表示，也可以用图形来表示。
思考2：如果A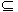B，且B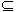C，则集合A与集合C的关系如何？
思考3：怎样表述a，{a}，{a，b}两两之间的关系？
知识探究（二）
考察下列各组集合：
（1）A={x|-3＜x≤3，x∈Z}与B={-2，-1，0，1，2，3}；
（2）A={x|x²-x-2=0}与B={-1，2}；
（3）A={y|y=x²，x∈R}与B={y|y=|x|，x∈R}。
思考，上述各组集合中，集合A与集合B之间的关系如何？
用子集概念对两个集合相等作进一步的数学描述：
如果集合A是集合B的子集，且集合B是集合A的子集，此时集合A与集合B中的元素是一样的，因此集合A与集合B相等，记作：A=B。
真子集定义：
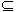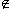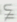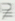对于两个集合A与B，如果AB，但存在元素x∈B，且xA，则称集合A是集合B的真子集，记作AB或BA。
例：写出下列集合的所有子集，并指出哪些是真子集。
（1）{a}；（2）{a，b}；（3）{a，b，c}；   （4）。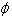
元素个数与集合子集个数的关系：n个元素，集合子集个数为2ⁿ。
例1：以下六个写法错误写法的个数（   ）
①{0}∈{0,1}   ②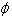{0}   ③{0,-1,1}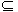{-1,0,1}
④0∈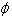   ⑤Z={整数}   ⑥{（0,0）}={0}
例2：写出满足{1,2}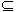A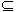{1,2,3,4}的所有集合A。
例3：设集合A={2，a²}，B={1，2，a}，若A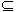B，求实数a的值。
例4：设集合A={x|-2≤x＜1}，B={x|0≤x-a≤1}，若B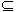A，求实数a的取值范围。
思考题：已知集合A={x∈R|x²+ax+1=0}，B={x|x＜0}，若A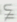B，求实数a的取值范围。
例5：已知集合A={x|(2x-1)/3＞1}，B={x|x+2a≥0}，若A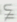B，求实数a的取值范围。
例6：已知集合A={x，1}，B={y，1，2}，其中x，y∈{1,2,…,9}，设集合M={（x，y）|A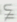B}，试确定集合M中共有多少个元素。

此内容正在抓紧时间编辑中，请耐心等待

孙老师

女，中教高级职称

优秀教师，高级教师职称。善于引导、启发学生，培养学生的逻辑思维，激发孩子对数学学习的兴趣。