课程内容

《函数的奇偶性》
1.观察下面两组图形，它们是否也有对称性呢？
(1)
 
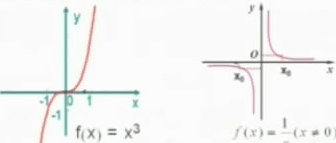
(2)

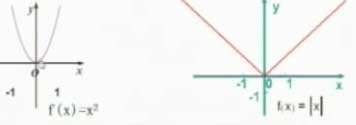
二、尝试探求
对于函数f(x)=x²，有f(-1)=(-1)²=1 f(1)=1 f(-1)=f(1) f(-2)=(-2)²=4 f(2)=4
f(-2)=f(2) f(-x)=(-x)²=x²
f(-x)=f(x)
结论：当自变量x认取定义域中的一对相反数时，对应的函数值相等，即f(-x)=f(x)
请你尝试给“偶函数”下一个定义：
如果对于函数f(x)定义域内的任意一个x。都有f(x)=f(x)，那么函数f(x)就叫偶函数。
对于函数f(x)=x³，有f(-1)=(-1)³=1 f(1)=1 f(-1)=-f(1)
f(-2)=(-2)³=8 f(2)=8
f(-2)=f(2)
f(-x)=(-x)³=-x³
f(-x)=-f(x)
结论:当自变量任取定义域中的两个相反数时，对应的函数值也互为相反数，即f(-x)=-f(x)

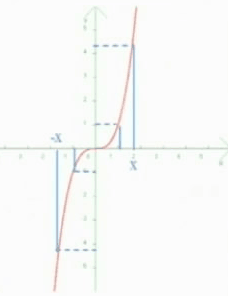
三、补充说明
(1)定义域关于原点对称式函数是奇、偶函数的先决条件。
(2)如果一个函数f(x)是奇函数或偶函数，那么我们就是说函数f(x)具有奇偶数。奇偶性是函数在整个定义域上的性质。
(3)若函数f(x)为奇函数，则f(-x)=-f(x)成立。
   若函数f(x)为偶函数，则f(-x)=f(x)成立。
(4)奇函数的图象关于原点对称。
   偶函数的图像关于y轴对称。
四、典例剖析
例1 判断下列函数的奇偶性
(1)f(x)=x+1/x
解：定义域是{x/x≠0}
∵f(-x)=-x-1/x=-(x+1/x)
即f(-x)=-f(x)
∴f(x)为奇偶数
(2)f(x)=1/x²+1
解：定义域是R
∵f(-x)=1/(-x)²+1=1/x²+1
即f(-x)=f(x)
∴f(x)为偶函数
(3)f(x)=√ x
解：定义域为[0.+x]
∵定义域不关于原点对称
∴f(x)为非奇非偶函数
(4)f(x)=2x+1
解：函数的定义域为R 但是f(-x)=2(-x)+1=-2x+1
∴f(-x)≠-f(x)且f(-x)≠f(x)
∴f(x)为非奇非偶函数
(5)f(x)=0
解：定义域为R
∵f(-x)=f(x)=0 又 f(-x)=-f(x)=-0=0
∴f(x)为既奇又偶函数
(6)f(x)=√1-x²/2-|x+2|
解：由1-x²≥0    -1≤x≤1
    |x+2|≠0   得x≠0且x≠4即-1≤x≤1且x≠0
∴定义域为[-1,0)U（0,1]
∴f(x)=√1-x²/2-(x+2)=√1-x²/x
∴f(-x)=-√1-(-x)²/-x=-√1-x²/x
五、归纳总结
1.根据奇偶性，函数可分为四类：
奇函数
偶函数
既奇又偶函数
非奇非偶函数
2.用定义判断函数奇偶性的步骤：
(1)先求出定义域，看定义域是否关于原点对称；
(2)再判断f(-x)或f(-x)=f(x)是否成立。
例2：已知函数f(x)是奇函数，当x＞0时，f(x)=x(1+x)，求x＜0时f(x)的表达式。
例3：已知f(x)为偶函数且在（0，+∞）上是减函数，试判断f(x)在（-∞，0）上是增函数还是减函数？并证明你的判断。