课程内容:
《一笔画》
十八世纪的时候,格尼斯堡附近的一条河中有两个小岛,两个小岛与两岸之间建有七座桥,当时流传这样一个难题:一个人怎样能够不重复的走过所有的桥?并且还能再回到出发点。这就是数学史上非常著名的“七桥问题”,当时的数学家欧拉听说了这件事情,他用A、B两点来表示小岛,用C、D两点来表示两岸,一个人如何不重复的走过七座桥并且再回到出发点的问题,也就转化成了如何一笔画出这样一个图形,也就是“一笔画”的问题。
定义:一笔画是指从图的一点出发,笔不离纸,每条边都只画一次而不重复。
例1.观察下面各图中的点,数一数它们分别与几条线相连?
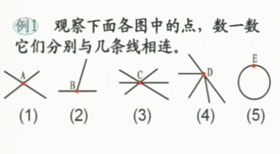
定义:与偶数条线相连的点叫做偶点。与奇数条线相连的点叫做奇点。
例2.下面图形各有几个奇点?各有几个偶点?这些图形能一笔画成吗?
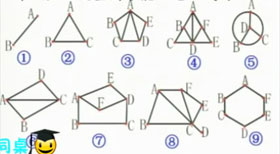
归纳:①全由偶点组成的图形可以一笔画成;画时可以从任何一点开始,最后仍回到这个点。
②只有两个奇点,其余都为偶点的图形,也可以一笔画成。但画时必须从其中的一个奇点开始,从另一个奇点结束。
例3.下面各图能不能一笔画成,为什么?如果能,请把画法用字母和箭头表示出来。
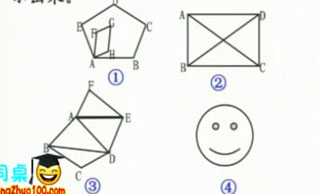
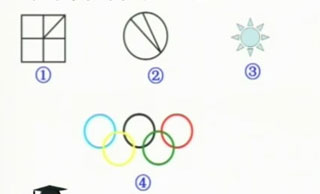
练习1:下列哪个图形可以一笔画出?
练习2:一辆洒水车要给某城市的街道洒水,街道地图如下,你能否设计一条洒水车洒水的路线,使洒水车不重复地走过所有的街道,再回到出发点?
练习3:下图是一个公园的品面图,能不能使游人走遍每一条路不重复?入口和出口又应该设在哪儿?
练习4:甲乙两个邮递员去送信,两人同时出发以同样速度走遍所有的街道,甲从A点出发,乙从B点出发,最后都回到邮局(C点)。如果要选择最短的线路,谁先回到邮局?
回到“七桥问题”,如果允许再架一座桥,能否不重复地一次走遍八座桥?这座桥应该架在哪里?